Perceptron is a video feedback engine with a variety of extraordinary graphical effects. It evolves colored geometric patterns, visual images and video streams into the realm of infinite details and deepens the thought.

Home page .................... https://perceptron.sourceforge.io

Download ...................... https://sourceforge.net/projects/perceptron

Gallery ........................... https://perceptron.sourceforge.io/gallery/index.html

Forum ............................ https://sourceforge.net/projects/perceptron/forums/forum/1256631

NEWS!

Perceptron 1.6.2 is the latest version available for download.

Almost four years since the version 1.6, Perceptron has been tested and slightly updated to correct some obvious bugs, and show the signs of life. The updates mostly affect Linux operating systems, so the current Windows and Mac users don't need to update their installed programs if they don't wish so. The Linux users can download the new Linux software archive from https://sourceforge.net/projects/perceptron/files/perceptron-1.6.2-linux.7z/download. Once the archive is unpacked, the user can enter the program directory, and execute ./run.sh script. The archive includes the Liberica Java Runtime Environment 8.

The webcam driver can cause errors with different consequences depending on your choice of the Java Runtime Environment, and other factors. If you don't have a webcam, you can disable it in the resource/Settings.txt file, by updating the line 55 to this:

webcam_support false

In the Settings.txt, all the users on all systems will find themselves sooner or later needing to change the Perceptron graphics resolution. Typically, we define it as 800-by-800-pixels square.

screen_width 800

screen_height 800

The previous Windows version of Perceptron with old Java is still functioning well, and includes a useful desktop link to the Settings.txt file.

https://sourceforge.net/projects/perceptron/files/Perceptron%201.6.1%20with%20Java%208.152%20for%20Windows.exe/download.

The new minimalistic installation program for Windows has a newer version of the Liberica Java Runtime Environment 8, and other Perceptron updates.

https://sourceforge.net/projects/perceptron/files/perceptron-1.6.2-windows-inno-setup.exe/download

Preferably, the user should install the program to any folder inside the user's home folder where Perceptron has all the read and write permissions.

The webcam driver supports IP cameras that are broadcasting from the internet. If you know any IpCam address and login details, you can insert them into the file resource/cameras.xml. See the sample file opened in this editor. The stream can be used in some of the coloring methods such as the edge-extend methods (E = 2 or 3) and image modes (L = 1 or 2). Perceptron does not broadcast its contents to the internet.

The public IP cameras included in this cameras.xml stopped broadcasting in the recent years. The IP camera support is now disabled in the Settings.txt file by default. You should first find some IP camera address to include and test in cameras.xml. If the video stream is unavailable, the Perceptron may print an error. This is safe in Windows, but it might lead to an unrecoverable state in Linux.

Any desktop systems where semi-transparent windows are not available in full manifest graphics errors inside the Screen Grabber window frequently. This has been corrected by avoiding the use of transparency on Linux if it's unavailable.

(OLD) If you are using the K-Lite Codec Pack, Smooth Video Project or some other codec pack, the webcam may fail to load if it accesses the webcam video stream that has been processed as the raw video by using FFDShow. Solution: reset the codec pack to the default settings, or avoid the processing of the raw video in the configuration, or use the LAV video processor instead of the FFDShow in the codec configuration for webcam stream.

Thanks. Animation recording capability has been provided in cooperation with Werner Randelshofer (https://www.randelshofer.ch/monte/) and it utilizes Monte Media library. Webcam recording facility has been provided by Bartosz Firyn (https://webcam-capture.sarxos.pl).

Perceptron explorations (from earlier versions) are summed up in this video...

In this little unmanned experiment, we see the live broadcast from European Space Agency through Perceptron.

Vortex of Subspace Delights

has opened for interstellar travel

and its full of JavaScripts that run in your browser

Geometric visual hallucinations

can be examined with this JavaScript applet,

an implementation of https://doi.org/10.1371/journal.pcbi.1002158

Background

The classical video feedback is an artistic technique that uses a video camera and a TV set. The camera and the TV set are connected by cable so that the TV set can display live images coming from the camera. The camera is directed at the TV screen – it is shooting the video of TV set together with the live images from its screen. With a slight delay, the TV set is broadcasting the video output from the camera. The TV screen develops a recognizable pattern, live image of screens within screens shrinking towards a bright point in the middle of the screen. By using a camera and a TV set only, we can see a variety of fractal spirals and specifically, saturation-related or pixel-related effects that stem from the electronic components. They are obtainable by rotating the camera around its axis slightly and zooming in. With a single mirror located next to the TV screen, we can additionally create fractal trees, and by adding even more mirrors, we can create complex IFS fractals. The effect of mirrors is equivalent to linear geometric transformations applied to the screen contents. Every geometric transformation in the video feedback cycle of visual data is applied repeatedly (recursively) to the screen contents. [1]

To the left (below), we can see my Web Camera pointing at the computer screen that is simultaneously displaying what the camera sees. To the right, I placed my finger in front of the camera and it was multiplied. Once you insert an object in front of the camera, the image is formed slowly and inwardly. The relationship between the size and position of my finger and the size and position of its first consecutive copy (slightly smaller one to the left) gives us the geometric transformation that is applied recursively to the screen contents in the video feedback cycle. The insertion of objects before the camera is also known as the “insertion of image into the video feedback flow” or as the “staining, tainting of flow” when a simple color is added to the flow and it colors the screen.

In the following experiment, I placed a small mirror next to the camera’s display on my computer screen, and a wondrous world was revealed. Can we learn to inhabit and explore such new world?

The display is constantly fluctuating because the camera is readjusting its sensitivity depending from the level of light in its view. When the fluctuations on the screen begin to increase, the camera also begins to readjust its sensitivity more wildly. Such behavior leads to possible chaos. The camera and the screen represent a dynamical feedback system. To see examples from other artists, see here, here, here and here. Summary of works from different artists can be found here below.

Perceptron

Perceptron simulates the essence of classical video feedback setup, although it does not attempt to match its output exactly. For example, it does not simulate the relationship between the TV set, the camera and the mirrors in space, or the effects due to electronic components. Instead, it uses a two-dimensional computer screen only in order to transform (morph) geometrically its contents. It applies any given complex function f(z, c) that maps each point of the screen to a new location. When repeated, the transformation produces a Julia fractal. This is unique to Perceptron. The selected (or typed in) function is coupled with the pullback effect (with rotation) that zooms in and out. See [2] for examples. This is intuitively similar to the camera zooming into the screen.

I morphed the beautiful girl photo recursively by applying f = z² - 0.66406214 - 0.24218677i and the pullback effect.

A set of coloring techniques produces Julia fractal contours (concentric quasi self-similar ovals), gradient shape visible as the shade on contours, and color saturation effects. The coloring techniques stem from the boundary condition check performed on the point z’ = f(z, c). The default type of check answers whether the point z’ is inside or outside the invisible limit circle with radius 1. In all, the coloring techniques are the outside coloring methods, the color gradients, the fade-to color modes, and the color filters.

With different coloring techniques, known Julia fractal begins to emerge.

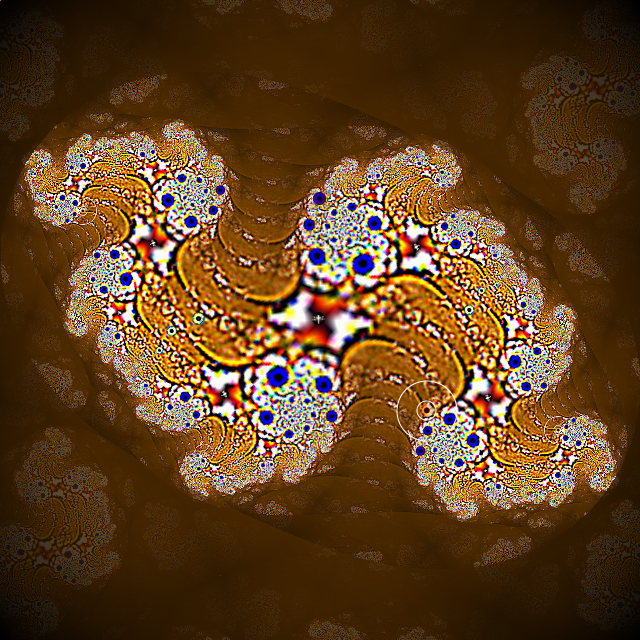
The “reflection transform” multiplies the resulting Julia fractal. It returns the points mapped outside of the screen dimensions back within the screen. This yields complex IFS fractals comprised of Julia fractal fragments (multiple exactly self-similar fragments). This is intuitively similar to the effect of mirrors, or linear geometric transformations, but can be more complex.

Video feedback fractals represent unique and remarkable class of fractals, a combined Julia and IFS kind of fractals. Some patterns such as those within the flickering Julia lake are chaotic. They can be static, alternating, or endlessly evolving in novel ways, which we call the “critical state”. Perceptron is both an artistic and a scientific visualization tool for these fractals. Here are some of the Perceptron’s animations… 1, 2, 3, 4, 5, 6, 7, 8. (The videos are extremely compressed to reduce size.)

References:

[1] https://users.math.yale.edu/public_html/People/frame/Fractals/Labs/VideoFeedbackLab/VideoFeedbackLab.html

[2] https://en.wikipedia.org/wiki/Conformal_map

Find out more online…

https://en.wikipedia.org/wiki/Video_feedback

https://en.wikipedia.org/wiki/Fractal

Distribution

Perceptron is a free, open source program written in Java (www.java.com) and licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Original author: Michael Everett Rule & friends, working on Caltech's course ACM95, chapter on conformal mapping. (since 2007; mrule7404 at gmail.com).

Documentation and the latest development: Predrag L. Bokšić (since 2010; junkerade at gmail.com).

How to run

Perceptron runs on any operating system that has Java environment installed. Java is a program that simulates a real computer. It is known as the Java virtual machine and it is used for running a wide variety of programs (that are somewhat simpler to design when they are designed for a virtual machine). The latest Windows installer of Perceptron installs 64-bit Java 8 into a program subfolder for use with Perceptron only. Alternative 32-bit version of Java is not bundled with Perceptron.

Manual Java installation for your operating system includes the following considerations. If you have a 64-bit operating system, you should install the 64-bit Java from Oracle. If you install the default Java from www.java.com, you will by default get the self-updating 32-bit version of Java Runtime Environment (JRE), which is commonly used with the internet browsers for running other Java applications on the old 32-bit operating systems.

If you are using Windows operating system, download and run the Windows installer version of Perceptron. By default, it will install Perceptron into your My Documents folder. I recommend that particular location, because you possess all the permissions to write to that folder. Access is required in order to save the artwork and to edit the settings file. When you run the program for the first time, Avast antivirus scans it for half a minute.

The Windows installer will put shortcuts on desktop to the Perceptron executable file and to the Perceptron Settings. By double-clicking Perceptron shortcut, the appropriate 32/64-bit version of Java should start automatically. The shortcut Perceptron Settings is used to edit the Settings.txt file in a text editor (if necessary).

The shortcuts to the helper applications Perceptron.exe and Perceptron 64.exe are installed in the Start Menu folder Perceptron. They are used to execute the Perceptron application itself – Perceptron.jar – by using the appropriate 32/64-bit Java version. The appropriate version for your system provides a considerable boost in performance. If Java is installed on your system properly, you can also double-click Perceptron.jar directly to start. The helper applications have failed to start in some cases in the past due to Java environment errors. Be free to reinstall the 64-bit version of Java if you have any further doubts and test Perceptron then. See some common issues on Windows machines.

If you are using Linux, download and unpack it manually. Perceptron uses any Java for Linux such as 64-bit OpenJRE version of Java, which is available from your distribution’s publisher. Java version 8 may not be available from your publisher; however, you can download it from Oracle. See help for OpenSuSE and Ubuntu. Once you unpack the Linux archive, enter the unpacked folder Perceptron. Click to run or edit the properties/permissions of Perceptron64.sh first and make that file executable by using chmod +x ./Perceptron64.sh. Right-click and drag this file from your file manager to your desktop. Linux will offer a menu to create a shortcut to the file. The folder Perceptron contains the icon file icon.ico that you can assign to the shortcut by right clicking the shortcut and editing its properties. Then you can use ./Perceptron64.sh in the unpacked folder immediately via command line or desktop shortcut.

For the manual Windows installation, use the following procedure. Download Java from Oracle as needed. Fetch the archive version of program from download section, unpack it and run the program. Unpack it to any folder where you have access, such as My Documents, or D:\ on Windows systems, or Home folder on Linux, etc. That will create a folder named Perceptron. Enter the unpacked folder Perceptron, right-click and drag the appropriate file Perceptron.exe or Perceptron 64.exe to your Desktop in order to create a desktop shortcut. The folder Perceptron contains the icon file icon.ico that you can assign to the shortcut by right clicking the shortcut and editing its properties, if necessary.

In you want to run the program manually, go to the console and execute java –d32 –jar Perceptron.jar or java –d64 –jar Perceptron.jar on a 32 or 64-bit operating system. In Linux, these commands are usually formatted as java –d32 –jar ./Perceptron.jar and java –d64 –jar ./Perceptron.jar. In Windows, it is possible to double-click the file Perceptron.jar directly and run it, but the success of this operation depends from the primary version or the last installed version of Java.

In the case of any unforeseen problems, you can try to reserve the additional memory space by executing the following command, java –d32 –Xms512m –Xmx1024m –jar Perceptron.jar or java –d64 –Xms512m –Xmx1024m –jar Perceptron.jar. (Do not artificially limit the available memory to a very small value, because the program will run into error.)

If you wish to see the source code, participate in the development and compile the project, then download the source code. Furthermore, install IntelliJ IDEA programming environment to open the Perceptron project folder.

Usage

After startup, it takes a few seconds for the first fractal image to appear in Perceptron. Fractals in Perceptron are evolving forever. They are never final. However, depending from the equation (complex function f(z, c)) and the selected reflection transform, some are changing a lot, while others are mostly static.

Keyboard Controls

Perceptron is controlled by keyboard, mouse and with a control window. Almost all keys on the keyboard are in use – they are associated with the program options. Read the on-screen help by pressing the key / (slash). Press F1 to open a help window. Take a look at some of the screenshots.

Mouse Controls

The mouse controls any one of the four basic cursors. At startup (as well as upon loading a preset), neither cursor is selected. Click left or right mouse button to select a cursor.

Red cursor: sets the parameter c of the complex function (e.g. f(z) = z² + c), (mimics the camera position).

Blue cursor: controls the pullback, (mimics the camera distance and rotation).

Yellow cursor: sets the color gradient parameters, offset and slope.

Dragonfly (black cursor): controls the amount and type of color filtering (contrast) in combination with the X switch.

The red cursor controls the parameter c with its position, c = (x, y). The center of screen represents the coordinate zero (0, 0), while the edges of a typical square screen are at about 1.1 units away.

The blue cursor controls the rotation and the pullback. If you rotate it around the coordinate zero, the whole fractal rotates, but at the same time, the parameter c rotates as well. If you move the blue cursor closer to the coordinate zero, you mimic the situation in which you move the camera away from the screen. This is analogous to the image of screens within screens diminishing in size and contracting towards the TV screen’s middle. If you move the blue cursor away from the coordinate zero, you zoom in, i.e. you simulate the camera approaching the screen. Press End to disable or enable the pullback.

It is best to see how the yellow cursor and the dragonfly cursor behave in practice. They control the application of the radial gradient, a matrix of shadow intensities that is used for the basic, gray-scale coloring of fractals. For example, if you move the yellow cursor to the lower left corner, you will see the classical Julia fractal in clear black and white. Other positions on the screen will reveal the effects of other coloring techniques, reflections, and even saturate the fractal with details. In combination with the X switch, the black cursor controls the shading of gray-scale Julia contours and if the fractal is full of lively colors, it has a large influence over the evolution of chaotic colored patterns.

Cursors are typically decorated with small circles (dots) that follow their motion. The cursor motion is slowed, because it smoothens the morphing of Julia fractal. It appears as though the cursor is dragging a weight on an elastic rope. Both features are optional and are adjustable by pressing =, - and ], [.

The activation of the rotating three-dimensional fractal Tree will bring up the additional, temporary set of 4 cursors that control the tree (its position and design). You can select any cursor by clicking left or right mouse button. The Tree is an artificially inserted IFS fractal for artistic purposes, which you can bring about when you press T. When you deactivate it, the tree-related cursors disappear.

The visibility of all active cursors can be switched off and on by pressing C.

Operation

The initial fractal is defined in the default preset file Perceptron\resource\presets\a.state. The default preset file is loaded automatically as the first preset file in folder Perceptron\resource\presets according to its name. In order for the Perceptron to function properly, there must be at least one, initial preset in the presets folder. The image file denoted in the preset must be present on your computer. If it is not found, the program will exit. If the image file is found, but other images denoted in other presets are not found, Perceptron will use the image denoted in the initial preset in combination with other presets whose respective image files were not found.

The screen resolution is given in the settings file, Perceptron\resource\Settings.txt. See the sample settings file. If you installed Windows installer version of Perceptron, the shortcut to the Settings.txt file is on your desktop. Otherwise, open the folder Perceptron\resource, hold the file Settings.txt with the right mouse button, drag it and drop it to your desktop. Double click the shortcut to edit the file manually. Old default resolution was 640 × 640 pixels and the current default is 600 x 600. Resolution tests.

Perceptron window can stretch without interrupting the program operation. If you want to reset window to default size and position, press Enter during operation. Pressing Enter is required when you change the resolution in the settings.txt file, because window size and position are otherwise reinstated at every startup and they remain the same unless you reset them by pressing Enter.

Remember to press / to get on-screen help, F1 to get a separate Help Window, Page Down to toggle Configuration Window and Page Up to see the Grabber Window (used for capturing the screen content and inputting it as a video stream or as a screenshot into video feedback cycle). Position of all windows is stored every time you exit Perceptron.

Do not change the contents of the resource folder unless you know what you are doing. You need the settings file, at least one preset, the image file denoted in the default preset, CrashLog.txt, cursors folder with the cursor images (icons), and possibly other files, especially if you are working with an experimental version.

The settings file contains expert parameters such as the presets folder and the image folder, which denote the locations from which Perceptron preloads all presets and all images at startup. The order of file loading is according to the names of files. The preloaded presets are accessible by pressing S or A. The image denoted in a preset is loaded when a particular preset is loaded and is used in the image modes (L = 1 or 2) and in the fractal mode (L = 0) combined with certain outside coloring methods (such as E = 3 or 4). The preloaded images are not necessarily denoted in any preset file. They can be selected by pressing M or N. When used, the selected image morphs on the screen (together with the mouse cursors) according to the selected program options, namely the complex function (also known as the “fractal map” or simply “equation”) and the “reflection transform”. You can load a single preset from any folder later during operation by pressing `. Also, you can load a single image from any folder later during operation by pressing \. All presets and images loaded in the course of operation are held in program memory. They are added to the preloaded presets and images, and are available by pressing S, A or M, N respectively.

The initial complex function (equation) used for drawing the fractal and morphing the image is denoted in the initial preset. If the equation is missing, then the default one will be used, z*z. Similarly, other parameters that are deleted from a preset acquire default values, if possible.

You can add your own complex functions (equations) to the long list of “maps” in the settings file. These equations are preloaded at startup and are available by pressing W or Q. You can type an equation in during runtime by pressing CTRL once, typing the equation and then pressing Enter. Press CTRL again to stop editing the equation. This way you will exit the equation editing mode, deactivate the text cursor and return the controls to the keyboard (return the default key assignments.) Hint: you can play with the colorful letters by typing text anywhere on the screen without pressing Enter (as to avoid entering a new equation made of silly text). The colorful letters represent the Salvia mode (press ; to disable or enable, and D to change the letter color scheme). The successfully typed-in and executed equations are added to the equations in memory (all of which become available by pressing W or Q), but are not saved to the hard disk otherwise, except for the current equation that will be saved if and when you save a preset.

The equation denoted in a preset and loaded together with a preset is active until you change it. Otherwise, it is not stored in memory and is not available by pressing W or Q. Some equations are tied with the keyboard keys – numbers (1, 2…) and function keys (F1, F2…). When you activate any of these, the given equation is added to the equations loaded in memory.

The equations in the settings file, those that you type in, as well as the ones stored in presets are in the form of f(z). For example, z*z gives the default Julia fractal. You can also write that particular equation as z^2, or zz. This is a well-known short form of z_new= z_old² + c.

The loaded equations, presets and images as well as other program parameters that can be switched with a single press of a button, are stored in lists that are repeating in circles. For example, the preset 0 is the first, initial preset. The image 0 is the first loaded image, the one denoted in the initial preset. The equation 0 is the first equation loaded into memory – the first “map” followed by equation in the settings file. When you type in and execute successfully any new equation, it is added to the end of the list in memory. By pressing W, you move forward and by pressing Q you move backward in the list of equations. Similarly, you can find presets and images in their respective lists.

The transitional image morphing occurs after you change certain parameters. It serves the esthetic purpose. The most precise way to operate Perceptron is to do things slowly and wait for the program to respond, for example, when you load or switch presets and images or type in equations. You cannot change the key parameters during the brief transitional period when the current image is morphing into the next one. The image switching works somewhat faster.

The save option appears when you press Space. It will enable you to save the state (preset file with .state extension) and the screenshots (two consecutive frames with extensions .in.png and .out.png). Sometimes it is knowledgeable to study the evolution of the evolving fractal displays by comparing differences between two consecutive frames. In some situations, the difference is not visible to the naked eye. The second image is finalized with image softening (press Y to change convolution). It is denoted with name.out.png. I recommend Picasa viewer for all your images, https://picasa.google.com.

If your artwork uses/displays an external image file that you loaded from your hard disk, the image file name will be saved (denoted) in the preset file. When you load the saved preset, Perceptron will look for that image file on your hard disk. However, if you plan to share your preset with other people, you must include the image file that you used. The only way to accomplish interoperability between different computers is to select an image file in advance and copy it anywhere within the Perceptron folder. Ideally, you should create a new subfolder to store the additional images. Later, you will run Perceptron, use the desired image file that is now located in the folder that you created within the Perceptron folder, and save the preset anywhere you like. When you give the preset to someone, include the subfolder with your image(s) and tell your audience to put the folder inside their Perceptron folder. This way, the path to the image together with the image file itself will be universally accessible on all computers.

The CapsLock is temporarily assigned as the save button during the equation editing mode (if for some reason, you wish to save a preset at that exact moment). Note that if you load a preset with the equation-editing mode enabled, the default key assignments will be temporarily unavailable until you press CTRL and exit the edit mode.

The saved presets are available by pressing ` (BackQuote), which calls the Open File menu, or by placing the saved presets in the Perceptron\resource\presets folder before the program starts. The name of the image file that was used at the time of operation is written in each preset. Make sure that the specified image file exists on your hard disk at the time of opening of preset. (Alternatively, a preloaded image from the Perceptron\resource\images folder that happens to be selected at that time will be used.)

The animation mode (movie recording) starts when you press Home. Menu will appear where you will be able to select the encoding method for movie encoding. The best movies are fast to record, but they constitute the extremely large files. The most practical movies are compressed - they are slow to generate, they do not possess high quality, but may be necessary. The animation mode will stop when you press Home again. The animation mode is slightly slower than the normal mode of operation. Remember to perform your planned actions slowly if you notice any dramatic decrease in performance.

Warning: The animation recording may produce extremely large movie file depending from the movie file type. Later, you can additionally compress your recorded movie file. Use the "conversion process" in other programs, such as Freemake Video Converter, StaxRip, or ffmpeg with one of its many frontends, such as Avanti. FFMpeg Drive was written specifically for Perceptron. Alternatively, try to execute a command such as ffmpeg –i .\movies\my_large_movie.mov .\movies\my_compressed_movie.mkv. The ffmpeg documentation is at the ffmpeg project homepage. See more examples.

Underlying multimedia support for Windows can be obtained here, here, here, or here. If you don’t have any video player already, Daum PotPlayer is technically the most sophisticated player. VideoLAN is the most popular at this moment, but Mulder’s SMplayer is the most successful player from a historical perspective, because it builds on the famous MPlayer project. Underlying multimedia support for OpenSuse Linux is here. SMplayer and VideoLAN are available for linux.

Advanced options for animation recording. The number of frames per second instructs the movie recorder to make a movie file that allegedly contains this number of images per second. Old television uses 25 to 30 FPS, which satisfies the demand for visual quality, and LCD/LED monitors work at 60 FPS, which puts the upper limit on FPS that you can display. The limiting factor is also the speed at which your computer can write all those frames into a movie file.

Fast recorder does not store all the frames that Perceptron is producing, because Perceptron speed varies in time depending from the type of fractal, size and other calculations that your computer is performing. Movie recorder instead, is similar to a camera pointing at the screen and recording the portion of your screen as it appears to you in real time. However, the "real time" cannot be captured continuously, but every N milliseconds. The value of 20 milliseconds does not capture the output from Perceptron entirely, if Perceptron is producing a video at more than 50 frames per second. If Perceptron is producing 25 images per second, this value can be set to 40. The formula is N = 1000 / number of frames per second = 40 milliseconds for 25 fps, or N = 20 for 50 fps.

Webcam capture is available by clicking the appropriate button in Configuration Window. This video stream is loaded in realtime into the video feedback cycle through image mode (press L and set the options 1 or 2) or in the modes that paint the contours of Julia fractals with an image - available by pressing E to set the options 2 or 3. Another menu in Configuration Window offers a list of available webcams (usually, the local USB webcam).

The IP cameras are webcams that are broadcasting from the internet. If you know any IpCam address and login details, you can insert it into the file resource/cameras.xml. See the sample file opened in this editor. The camera will be listed then in the Configuration Window menu. The stream is then used in some of the coloring methods such as the edge-extend methods (E) and image modes (L). Perceptron does not broadcast its contents to the internet.

Live grabber refers to continuous screen grabbing and streaming into video feedback flow. First you need to activate the grabber window in order to define the grabbing area and then you need to press the button in the middle of the grabber window to save this area. Live grabber is then available by clicking the appropriate button in Configuration Window. Non-live grabbing refers to taking a single screen snapshot.

Algorithm

Understanding of the Perceptron's algorithm gives perspective on both the science of video feedback fractals and the meaning of its numerous options. Some options are best explained through usage. See the brief visual guide to the algorithm.

Program options

Boundary Condition (R) – the boundary condition for points z’.

0 Rectangular Window (as the “limit circle”)

1 Limit Circle (for classical Julia sets)

2 Elastic Limit Circle (the limit circle size is tied with the blue cursor)

3 Horizontal Window

4 Vertical Window

5 Inverse Oval Window (the inverse check on oval window)

6 No Window (move on to outside coloring)

7 Framed Window (with a colored frame)

8 Convergent bailout condition (for Newton fractals)

Outside Coloring Method (E) – what to do with the points z’ that are “beyond” according to the boundary condition check.

0 Fill With Fade-to Color

1 Edge Extend (pass on the color for points within a large screen)

2 Just Pass on the Color

3 Paint With Image (loaded image appears on fractal contours)

4 Paint With Image II (image with soft edges)

5 Fuzzy (a type of color average around the location z’)

Reflection Transform (I) – the contraction of points z’ back within the screen limits.

Let z’ = (x, y), while Width and Height denote the screen dimensions (W, H). The point z’ can

reach the positions between 0 and W – 1, and 0 and H – 1. Make x and y positive.

0 Shrink z’ to x = W – 1 – x modulo W, and y = H – 1 – y modulo H.

Perform the pixel interpolation (rounding of pixels and enhancement of image quality).

1 If x / W is even, x = x modulo W, otherwise x = W – 1 – x modulo W.

If y / H is even, y = y modulo H, otherwise x = W – 1 – x modulo W. Without the interpolation, but in use by the convolution procedure that adds a layer over images (for softening).

2 Same as 1, but with pixel interpolation.

3 x = x modulo W / 2, y = y modulo H / 2. With interpolation.

4 If x > W – 1, x = x modulo W, otherwise x = W – 1 – x modulo W.

If y > H – 1, y = y modulo H, otherwise y = H – 1 – y modulo H. With interpolation.

5 If x < W, x = x modulo W / 2, otherwise x = W – 1 – x modulo W.

If y < H, y = y modulo H / 2, otherwise y = H – 1 – y modulo H. With interpolation.

6 If x / W is even, x = x modulo W / 2, otherwise x = W – 1 – x modulo W / 2.

If y / H is even, y = y modulo H / 2, otherwise x = W – 1 – x modulo W / 2. Performs the additional operation of making x, y positive, because they could become so large (>2147483647) that they wrap around and come up as negative numbers. With interpolation.

7 If x / W is even, x = x modulo W / 2, otherwise x = (W – 1) / 2 – x modulo W / 2.

If y / H is even, y = y modulo H / 2, otherwise x = (W – 1) / 2 – x modulo W / 2. Performs the additional operation of making x, y positive, because they could become so large (>2147483647) that they wrap around and come up as negative numbers. With interpolation.

Color Gradient (G) – the color added to the points z’ that are “beyond” according to the boundary condition check.

0 No Gradient (do nothing)

1 Simple Gradient (gradient affects the color)

2 Accented Gradient (accent color plays an additional role)

Gradient Shape (‘) – the shape of the two-dimensional shadow used for basic gray-scale coloring.

The gradient shape can be visible on the contours of a typical Julia fractal, which in turn can be uniformly colored (without any indication of the gradient shape), or varied (which shows the gradient shape). Each of 10 gradients was made by the calculation of various functions of two variables. The default gradient (0) is the radial shadow, black in the center and gradually whiter towards the perimeter.

Suppose that the Julia set is a circle. When you change the proportions of screen (by adjusting the screen resolution), the Julia fractal becomes an ellipse. The radial shadow also becomes elliptic. This behavior is considered more natural for a video feedback system, because its displays depend from the shape of the screen. The contours of the Julia fractal behave similarly to the images of screens within screens in the classical video feedback setup.

Gradient Direction (K) – whether the gradient shade is going from black to white or from white to black.

Fade Color Mode (F) – the fade-to color mixed with the existing color of the point z’ outside the limit circle.

0 Black

1 White

2 Mid-Screen Pixel Hue (select the color from the middle of the screen)

3 Not Mid-Screen Pixel Hue (select the negated color value of the mid-screen pixel)

4 Mid-Screen Pixel Hue Rotate (rotate the hue through HSV color spectrum and combine it with the mid-screen pixel color)

5 Hue Rotate (rotate the hue through HSV color spectrum)

Dampen Fade-to Color (V) – a small dampening of fade-to color.

Color Accent (H) – choose the accent color.

Color Filters (X) – the contrast enhancements.

0 None (do nothing)

1 RGB (various filters and color functions play a role)

2 Mush (various filters and color functions play a role)

Partial Inversion (Insert) – partial inversion of colors affects the fractal contours; black can become white and white black.

Thanks to the total color inversion that affects the entire visual image in each cycle, we have the interchanging Julia contours, but consequentially the Julia lake flickers. The partial inversion does not affect the flicker. It acts as the conventional color inversion of the current screen contents.

Total Inversion (J) – disables the fundamental color inversion.

The flickering of the Julia lake stops, but the contours disappear as well. The visibility of fractals depends from the fractal map (since some Julia fractals do not possess any lakes), and the presence of other images on the screen (notably the screen cursors).

Initial set (B) – enable or disable the treatment of cursors and text as the persistent initial set.

The mouse cursors, the letters, as well as the text cursor in the equation editing mode are present on the screen on top of the fractal. They are “persistent”/unchangeable, but the video feedback inputs them and morphs them together with all other contents of the screen equally. As such, they are useful for color seeding and demonstrating the nature of video feedback flow.

Convolution (Y) – methods for Gaussian image blurring (softening).

This option has the potential to improve image quality. Values are 0, 1, 2, 3. Zero is the fastest option. Other values may require adjustment of the color filter weight by using left and right arrow keys. Notice that the pixel interpolation methods are a part of reflection transformations (I). Option 3 represents full convolution. Options 1 and 2 are reduced mutant cases.

Autorotation, Autopilot and Wanderer (, . p Delete) – continuous random change of different parameters.

Fun () – for speed purposes, we do not time your usage of Perceptron.

Inserting the images into the flow

One of the fascinating research options is to insert different images, live feed from a web camera, or geometric patterns produced in various processes into the video feedback flow. The rotating three-dimensional fractal Tree is one such insertion. It enables one to understand the morphing of images under the given geometric transformations. The insertions allow us to understand the dynamics of fractals and discover brand new patterns. If you have any idea what to insert into the flow and how, or wish to expand the theory of video feedback fractals, please join the forum of send us an email to junkerade at gmail.com.

Resources - Chaos theory

• Series of online courses at www.complexityexplorer.org – expanding series of free courses by Santa Fe institute.

• Material available for the course Agent Based Modeling of Complex Adaptive Systems by University Delft at https://goo.gl/GoXK7X - "...a dynamic network of many agents (which may represent cells, species, individuals, firms, nations) acting in parallel, constantly acting and reacting to what the other agents are doing”.

• Course by Cornell University in nonlinear dynamics and chaos https://goo.gl/bTw4G2 - classical college lectures by Steven Strogatz featuring heavy mathematical analysis.

• Popular forum at www.fractalforums.com – a forum on every possible topic related to chaos or fractals, which now includes Chaos TV.

• NetLogo simulation environment ccl.northwestern.edu/netlogo – playing environment for the study of various problems in complexity science.

• Algorithmic Beauty of Plants at https://algorithmicbotany.org - computational design of plants.

• Graphics programming language www.processing.org – programming language for easy access to graphics functionality, visualization and many artistic effects.

• “Complexity” by Melanie Mitchell (Oxford 2009) – a guide, easy general textbook on many different topics approximately covered by complexity science.

• “Chaos: Making a New Science” by James Gleick (Penguin Books 2008, original 1987) – entertaining reportage on chaos, now a history book for easy reading.

• “Chaos and Fractals” by Heinz-Otto Peitgen, Hartmut Jürgens and Dietmar Saupe (second edition by Springer 2004) – a graphical and mathematical exploration of fractals that offers clearly laid-out story designed to be understandable in full.

• “Sync” by Steven Strogatz (Hyperion 2004) – essential reading on the synchronization and other topics for the masses.

• “The Nonlinear Universe” by Alwyn C. Scott (Springer 2007) – advanced overview of a variety of research areas where nonlinear science played some role.

• “Fractals and Chaos Simplified for the Life Sciences” by Larry S. Liebowitch (Oxford 1998) – collection of definitions, diagrams and formulas from the complexity science.

• SPACE-TIME DYNAMICS IN VIDEO FEEDBACK
Physica, 1984
James P. Crutchfield
Video feedback provides a readily available experimental system to study complex spatial and temporal dynamics. This article outlines the use and modeling of video feedback systems. It includes a discussion of video physics and proposes two models for video feedback dynamics based on a discrete-time iterated functional equation and on a reaction-diffusion partial differential equation. Color photographs illustrate results from actual video experiments. Digital computer simulations of the models reproduce the basic spatio-temporal dynamics found in the experiments. https://www.vasulka.org/Kitchen/PDF_Eigenwelt/pdf/191-207.pdf

• Optics-group website https://www.physics.gla.ac.uk/Optics/play/fractalVideoFeedback/

• Dr. Tom's video feedback experiments https://members.tripod.com/professor_tom/galleries/video/index.html

Be Intuitive!